An efficient density matrix renormalization group algorithm for chains with periodic boundary condition

Abstract

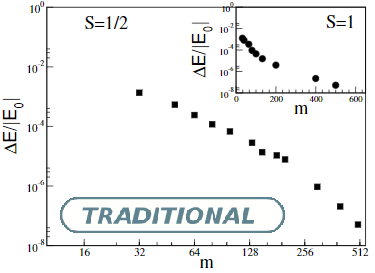
The Density Matrix Renormalization Group (DMRG) is a state-of-the-art numerical technique for a one dimensional quantum many-body system; but calculating accurate results for a system with Periodic Boundary Condition (PBC) from the conventional DMRG has been a challenging job from the inception of DMRG. The recent development of the Matrix Product State (MPS) algorithm gives a new approach to find accurate results for the one dimensional PBC system. The most efficient implementation of the MPS algorithm can scale as O($p \times m^3$), where $p$ can vary from 4 to $m^2$. In this paper, we propose a new DMRG algorithm, which is very similar to the conventional DMRG and gives comparable accuracy to that of MPS. The computation effort of the new algorithm goes as O($m^3$) and the conventional DMRG code can be easily modified for the new algorithm.

Received: 2 August 2016,  Accepted: 12 October 2016; Edited by: K. Hallberg; DOI: http://dx.doi.org/10.4279/PIP.080006

Cite as: D Dey, D Maiti, M Kumar, Papers in Physics 8, 080006 (2016)

This paper, by D Dey, D Maiti, M Kumar, is licensed under the Creative Commons Attribution License 3.0.